At the beginning of the 17th century, the dawn of the Age of Enlightenment in Europe, the need for correct and speedy calculations was greater than ever. Scientific fields including astronomy and geodesy were blossoming, as were the fields of architecture and trade.
The carrying of tens is usually the biggest source of errors in written arithmetic. Even when calculating with simple arithmetic tools, such as Napier’s rods, carrying tens must be done mentally.

John Napier of Scotland created this manually operated calculating tool in 1617 — it uses multiplication tables to aid in multiplying and dividing numbers quickly.
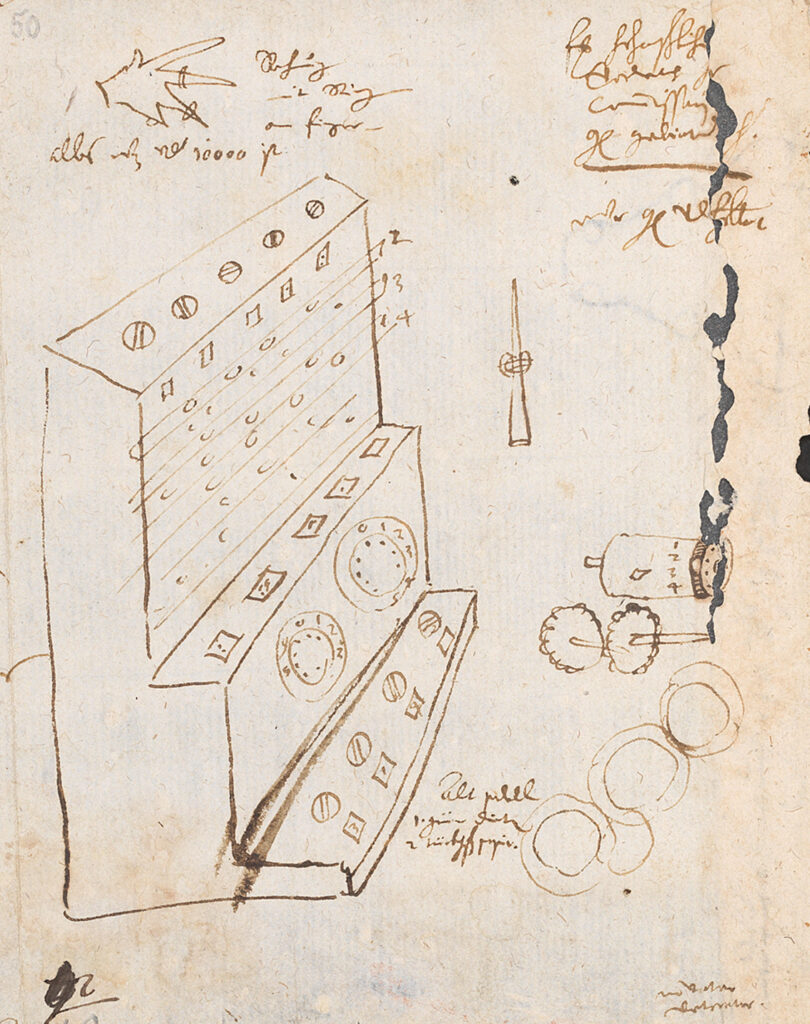
Around the same time, Wilhelm Schickard, a young professor of Hebrew in Tübingen, Germany, was also ruminating on arithmetic. Schickard had many talents and was interested in astronomy, geodesy and mathematics.
In 1617, he met Johannes Kepler, a fellow astronomer and mathematician, who had come to Tübingen to defend his mother in a witch trial (which she won). Together they developed the idea of a calculating machine that could calculate without error. Schickard, who was also a gifted mechanic, began designing and building the machine and completed it in 1623. He called it the Rechenuhr, or calculating clock.

He tested his machine extensively and wrote Kepler enthusiastically in a letter: “You would laugh out loud if you were there and saw how it increases the digits on the left all by itself when it exceeds a ten or a hundred, or takes something away from them when it subtracts.“
Schickard’s invention was a major step in the mechanization of arithmetic. Never before had an inventor constructed a calculating machine that could mechanically add and subtract up to six digits.
Unfortunately, no one today has ever seen that first calculating machine. Kepler’s copy was lost during the 30 Years’ War, which raged in Europe from 1618 to 1648, and Schickard’s own prototype burned up in his workshop before he died in 1635. What we know about Schickard’s invention comes from his surviving drawings, which were discovered in the mid-20th century and have since been used to create reconstructions.

A competitor arises

The earliest calculating device still in existence today was invented by Blaise Pascal in 1645.
Pascal was just 19 when he designed the calculating machine, made with the help of clockmakers in Rouen, France. His father, a tax official in Normandy, presented the machine to his superior, the chancellor Pierre Séguier, who obtained a royal privilege (akin to a patent) for Pascal. Several Pascalines were produced that could add and subtract mechanically in a similar way to the machine designed by Schickard. Although the Pascaline was not the first calculating machine, it was by far the most elegant. Thanks to its mechanical implementation, the carrying of tens was easy.
In Schickard’s calculating machine, the force required to move all the digits is added together for the secondary carrying of tens, but in the Pascaline, the force is stored at each digit. Thus, in the calculation 999,999 + 1 = 1,000,000, the carrying of tens is activated like a row of dominoes — each one triggers the next. This was made possible by a small weight that rose when a digit was placed. At 9, the weight reaches its highest position. The next addition triggers a carry and releases the weight, and gravity takes care of all secondary carrying.

This ingenious idea was used in a similar way throughout the 19th century to carry tens in mechanical adding machines. Both Schickard’s and Pascal’s machines were able to add and subtract, but devising how to multiply or divide mechanically eluded them.
The next level
Carrying tens in cases of multiplication and division was much more complicated. One could mimic multiplication by performing multiple addition functions and division by multiple subtraction functions. But four-function calculators required mechanical number storage to return a multiplication or division solution in one turn of the crank.
Gottfried Wilhelm Leibniz, who built the first mechanical four-function calculating machine in the late 17th century, recognized this problem. He was the first to develop such an intermediate storage device for carrying tens.

After Leibniz’s invention, other innovators conceived, developed and built very different technical solutions for carrying tens in four-function calculating machines. This major cultural-historical development of mechanical calculating machines did not come from one spontaneous idea, but was the result of the deliberations of many ingenious inventors.
Charles Xavier Thomas de Colmar was one of the first to succeed in constructing a four-function calculating machine in 1820. His Arithmomètre went into series production in 1855, becoming the first commercially successful computing machine, and was sold around the world for 70 years. His idea of building a robust stepped-drum mechanism became the cornerstone of European calculating machine manufacturing.
He presented a luxe Piano Arithmomètre, which was able to calculate results of up to 30 digits, at the 1855 Universal Exhibition in Paris.

Accompanied by much smaller pinwheel calculating machines that came onto the market around 1890, the technology of Thomas de Colmar’s Arithmomètre prevailed until the rise of the digital calculating machine in the mid-20th century.
The development of semiconductors, which led to the pocket calculator and the modern computer, has since overshadowed the 400-year history of mechanical calculators. But these early machines are still fascinating, showing how inventive mathematicians have been in pursuing perfect calculations — the essential basis of all quantitative sciences.
Many of these calculating machines are functional and on display in the Arithmeum at the University of Bonn, Germany. It remains to be seen whether our modern computers will still work as well in four centuries as the Pascaline does today.
Read more
Sign up to keep up to date with ReThink Q.







